Uniwersytet Komisji Edukacji Narodowej, Kraków
Instytut Bezpieczeństwa i Informatyki, Zakład Fizyki Komputerowej i Informatyki Kwantowej


University of The National Education Commission, Krakow, Poland
The Institute of Security and Computer Science, Department of Computer Physics and Quantum Informatics
                Dr Łukasz T. Stępień                          e-mail:    e-mail



Selected   Publications

1. Ł. T. Stępień, (Co-Authors: Henryk Arodz and Robert Pelka): H. Arodz, R. Pelka and L. Stepien, "Perturbations of planar interfaces in Ginzburg-Landau models" , Acta Phys. Pol. B 32 , (4), 1173 (2001).
2. Ł. Stępień, (Co-Authors: Danuta Sokalska and Krzysztof Sokalski): L. Stepien, D. Sokalska and K. Sokalski "The Bogomolny decomposition for systems of two generalized nonlinear partial differential equations of the second order", , J. Nonl. Math. Phys., 16, No. 1, 25 (2009).
3. Ł. T. Stępień, "Some decomposition method for analytic solving of certain nonlinear partial differential equations in physics with applications" : J. Comp. Appl. Math., 233, (6), 1607 (2010).
4. L. T. Stepien, "Selected methods of software engineering in teaching of some school subjects" , in the book "Information technologies in teacher's methods" (Editors: Jacek Migdalek and Wojciech Folta), KSIEGARNIA AKADEMICKA, Krakow 2010 (in Polish).

5. "On the consistency of Peano's Arithmetic System" , (Co-Author: Teodor Stepien): T. J. Stepien and L. T. Stepien, Bull. Symb. Logic 16, No. 1, 132 (2010). http://www.math.ucla.edu/~asl/bsl/1601-toc.htm

This above link leads to the Proceedings of the Conference "2009 European Summer Meeting of Association for Symbolic Logic, Logic Colloquium'09" (July 31 - August 5, 2009, Sofia, Bulgaria) . There, on the page 132, is published the abstract of the talk "On consistency of Peano's Arithmetic System", delivered by me, commonly with Dr Teodor Stepien, at "Logic Colloquium 2009" (July 31 - August 5, 2009, Sofia, Bulgaria). During this talk, we presented a sketch of the proof of the consistency of Peano's Arithmetic System (of course, the FULL proof was constructed by us before the mentioned Conference "Logic Colloquium 2009"). This proof is absolutely elementary, i.e. there have been used ONLY the axioms of first-order logic and the axioms of Peano's Arithmetic System.  

In other words: the consistency of the Arithmetic System is provable within this System.
The paper including this proof, was published in Journal of Mathematics and System Science : T. J. Stępień, Ł. T. Stępień, "On the Consistency of the Arithmetic System", J. Math. Syst. Sci. 7, No.2, 43-55 (2017) http://www.davidpublisher.org/Public/uploads/Contribute/58d876b1d91a2.pdf ; arXiv:1803.11072 .
(In the literature of the subject, one often tells that Gödel's Second Incompleteness Theorem tells that one cannot prove the consistency of the Arithmetic System within this System, UNLESS the Arithmetic System in inconsistent. )


6. "Atomic entailment and classical entailment" , (Co-Author: Teodor Stepien): T. J. Stepien and L. T. Stepien, Bull. Symb. Logic 17, No. 2, 317-318 (2011). http://www.math.ucla.edu/~asl/bsl/1702-toc.htm

This above link leads to the Proceedings of the Conference "2010 European Summer Meeting of Association for Symbolic Logic, Logic Colloquium 2010" (July 25 - 31, 2010, Paris, France). There on the pages 317-318 is published the abstract of the talk "Atomic entailment and classical entailment". We presented, during this talk, the definitions of: atomic entailment and classical entailment. Atomic entailment allows to avoid the paradoxes of material implication. The problem of the paradoxes of material implication, has been known, as the problem of relevance (sometimes called also as "relevance problem"), since 400 B.C. We showed also the connection between atomic entailment and classical entailment and we presented the theorem, saying that Peano's Arithmetic System can be based on atomic logic.

The full paper entitled "Atomic Entailment and Atomic Inconsistency and Classical Entailment" , was published in Journal of Mathematics and System Science (T. J. Stepien and L. T. Stepien, J. Math. Syst. Sci. 5, No.2, 60-71 (2015)): http://www.davidpublisher.com/index.php/Home/Article/index?id=235.html ; arXiv:1603.06621 .

the keywords: conditionals, conditional logic, entailment, entailment problem, logic of conditionals, non-classical logic, paradoxes of material implication, relevance, relevant logic

In the next full paper, entitled "The Formalization of The Arithmetic System on The Ground of The Atomic Logic" and published in Journal of Mathematics and System Science (T. J. Stepien and L. T. Stepien, J. Math. Syst. Sci. 5, No.9, 364-368 (2015)): http://www.davidpublisher.org/index.php/Home/Article/index?id=18008.html ; arXiv:1603.09334 ,
we have showed that the classical Arithmetic can be based on the Atomic Logic.

The abstract of this paper, was sent to Logic Colloquium 2015 (2015 European Summer Meeting of the Association for Symbolic Logic, Helsinki, Finland, August 3 - 8, 2015). This abstract was published in The Bulletin of Symbolic Logic: T. J. Stepien and L. T. Stepien, "The formalization of the arithmetic system on the ground of the atomic logic" , Bull. Symb. Logic 22 , No. 3, 434 - 435 (2016).
https://doi.org/10.1017/bsl.2016.22


7. , Ł. T. Stępień, "On Bogomolny Decompositions for the Baby Skyrme Models" , L. T. Stepien in: Geometric Methods in Physics, XXXI Workshop, Białowieża, Poland, June 24–30, 2012, Series: Trends in Mathematics, Kielanowski, P.; Ali, S.T.; Odesskii, A.; Odzijewicz, A.; Schlichenmaier, M.; Voronov, T. (Eds.), pp. 229 - 237, Birkhäuser Basel 2013.
This paper was based on a talk, delivered at "XXXI Workshop on Geometric Methods in Physics" (24-30.06.2012, Białowieża, Poland). In this paper, the so-called Bogomolny decompositions (the keywords: Bogomolny equation, Bogomol'nyi equation, Bogomolny equations, Bogomol'nyi equations, Bogomolny argument, Bogomol'nyi argument), for baby Skyrme models: restricted and full one, in (2+0)-dimensions, have been derived.
The baby Skyrme model is some analogon of the Skyrme model. This last one can be considered as some generalization of the nonlinear "sigma" model ("O(3) model"): in order to avoid the consequences of Derrick-Hobart theorem (the keywords: Derrick theorem, Derrick-Hobart theorem, Derrick argument, Derrick's argument, (Derrick) scale argument), there in the lagrangian, beside the nonlinear "sigma" term, the so called "Skyrme term" appears.


8. "The Scope of the Structural Completeness in the Class of all Over-Systems of the Classical Functional Calculus with Identity" , (Co-Author: Teodor Stepien): T. J. Stepien and L. T. Stepien, J. Math. Syst. Sci. 4, No. 6, 411-420 (2014). http://www.davidpublisher.com/index.php/Home/Article/index?id=1188.html

In this paper, the scope of the structural completeness in the class of all over-systems of the classical functional calculus with identity, was established.


9. Ł. T. Stępień, "The Existence of Bogomolny Decompositions for Gauged O(3) Nonlinear "Sigma" Model and for Gauged Baby Skyrme Models" , Acta Phys. Pol. B46, No. 5, 999 - 1023 (2015). DOI: http://dx.doi.org/10.5506/APhysPolB.46.999


10. Ł. T. Stępień, "Bogomolny equation for the BPS Skyrme model from the strong necessary conditions" , J. Phys. A49, 175202 - 175208 (2016). DOI http://dx.doi.org/10.1088/1751-8113/49/17/175202


11. Ł. T. Stępień, "Bogomolny equations in certain generalized baby BPS Skyrme models", DOI https://doi.org/10.1088/1751-8121/aa92d9 J. Phys. , A51 , 015208 (2018)


12. Ł. T. Stępień, "On Bogomolny Equations in The Skyrme Model", Acta Phys. Pol. B50 , 65 (2019), DOI:10.5506/APhysPolB.50.65


13. Ł. T. Stępień, "Bogomolny equations for the BPS Skyrme models with impurity" , Journal of High Energy Physics 2020, No. 6, 065105 (2020). https://link.springer.com/content/pdf/10.1007/JHEP09(2020)140.pdf


14. Ł. T. Stępień, "On some exact solutions of heavenly equations in four dimensions" , AIP Advances 10, No. 9, 140 (2020). https://doi.org/10.1063/1.5144327


15. Teodor J. Stepien, Lukasz T. Stepien, http://www.davidpublisher.org/Public/uploads/Contribute/5fa38c7b876bf.pdf an abstract "On the Inconsistency of Classical Propositional Calculus", Journal of Mathematics and System Science , vol. 10, No. 1, 13 - 14 (2020).


16. Teodor J. Stepien, Lukasz T. Stepien, an abstract of the talk "On the Inconsistency of Classical Logic" , delivered by me at The LXVI Cracow Conference on History of Logic (3 - 4 November 2020, Cracow)

17. Łukasz T. Stepien, "Some Exact Solutions of ABC and Martinez Alonso-Shabat Equations." J. Geom. Symmetry Phys. 66, 47 (2023).

18. Ł. T. Stępień, "Strong Necessary Conditions and the Cauchy Problem", Symmetry, 15 (9), 1622 (2023).

19. Ł. T. Stępień, paper "On the Inconsistency of: The Classical Propositional Calculus and Its Metatheory" , includes a proof of inconsistency of the Classical Propositional Calculus; accepted to be published in Journal of Mathematics and System Science ; PUBLISHED in preprints.org - DOI: 10.20944/preprints202312.0602.v1


Press information, among others, about the talk "On consistency of Peano's Arithmetic System", delivered by Dr Teodor J. Stepien and me, on 9th January 2013 , in Chair of Computer Science and Computational Methods (The Pedagogical University of Cracow)
The feuilleton "On the consistency of mathematics" (in Polish) of Professor Ryszard Tadeusiewicz (AGH University of Science and Technology), published in "Gazeta Krakowska" ("Cracow Newspaper") (9th January 2013), accessible on http://www.gazetakrakowska.pl/artykul/735525,o-niesprzecznosci-matematyki,id,t.html?cookie=1. This feuilleton was published also on   http://www.agh.edu.pl/aktualnosci/info/article/o-niesprzecznosci-matematyki-felieton/

(Dr Teodor J. Stepien and me, thank very much to Professor Ryszard Tadeusiewicz, for writing this feuilleton).





A list of some previous publications of Teodor J. Stepien (Teodor Stepien):

1. A Survey Of Minor Wajsberg's Results Concerning Fragmentary Systems Of The Classical Propositional Calculus, Bulletin of the Section of Logic , vol. 2, Issue 2, 103 - 106 (1973)

2. Every Two-Valued Propositional Calculus Has the Interpolation Property (with Z. Dywan), Bulletin of the Section of Logic , vol. 9, Issue 4, 152 - 153 (1980)

3. Lindenbaum's extensions (with A. Biela), Bulletin of the Section of Logic , vol. 10, Issue 1, 42 - 47 (1981)

4. System S̄, Bulletin of the Section of Logic , vol. 10, Issue 2, 75 - 78 (1981)

5. Craig-Gödel-Lindenbaum's Property and Sobocinski-Tarski's Property in Propositional Calculi, Bulletin of the Section of Logic , vol. 10, Issue 3, 116 - 120 (1981)

6. Lindenbaum's extensions (with A. Biela), Reports On Mathematical Logic , No. 15, 9 - 11 (1983)

7. System S̄, Reports On Mathematical Logic , No. 15, 59 - 65 (1983)

8. A sufficient and Necessary Condition for Tarski's Property in Lindenbaum's Extensions, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, (currently: Mathematical Logic Quaterly) , vol. 30, 447 - 453 (1984)

9. On Number of Lindenbaum's Oversystems of Propositional and Predicate Calculi, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, (currently: Mathematical Logic Quaterly) , vol. 31, 333 - 344 (1985)

10. Logic Based on Atomic Entailment, Bulletin of the Section of Logic , vol. 14, Issue 2, 65 - 69 (1985)

11. On The Uniqueness of the Lindenbaum Extension, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, (currently: Mathematical Logic Quaterly) , vol. 34, 463 - 469 (1988)

12. First-Order Theories without Axioms, Reports On Mathematical Logic , No. 23, 67 - 70 (1989)

13. Single-Axiom Systems, Reports On Mathematical Logic , No. 23, 67 - 70 (1989)

14. Minimal Systems, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, (currently: Mathematical Logic Quaterly) , vol. 36, 423 - 430 (1990)

15. A Note on Formalisations of First-order Theories, Reports on Mathematical Logic , No. 27, 19-28 (1993)

16. Derivability, Reports on Mathematical Logic , No. 33, 79-98 (1999)




45 Zjazd Fizyków Polskich, 13 - 18 wrzesnia 2019 r., Kraków, o zjezdzie mozna przeczytac tutaj

The branch of physics, in which I am engaged (in Polish): theoretical physics, especially nonlinear field theory (among others, exact solutions as instantons, solitons etc.)


Tzw. solitony, bardzo ciekawe rozwiązania nieliniowych równań ewolucji czasowej.


I found these two below figures of solitons on Prof. Alex Kasman's soliton page:
http://math.cofc.edu/faculty/kasman/SOLITONPICS/index.html

and I placed it here ( with Prof. Kasman's consent ):

Tak się zderzaja tzw. solitony równania KdV.


A oto rownanie KdV:   No Title
u,t -6 u u,x + u,xxx = 0
(1)


File translated from TEX by TTH, version 3.85.
On 09 Feb 2009, 01:12.

Inne rownanie solitonowe, to rownanie sinus-Gordona:

No Title
u,tt - u,xx = sin(u)
(1)


File translated from TEX by TTH, version 3.85.
On 09 Feb 2009, 19:07.

Dla przyzwyczajonych do standardowych oznaczen pochodnych czastkowych, to samo rownanie sinus-Gordona (czasem nazywane rowniez rownaniem "sine-Gordona"), co powyzej, zapisane wlasnie w tradycyjnych oznaczeniach pochodnych czastkowych:



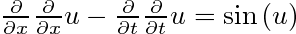
Jak widac, jednak troszke sie rozni od tej pierwszej wersji: lewa strona ma znak przeciwny do lewej strony tamtego rownania. Bierze sie to stad, ze w pierwszym rownaniu uzywamy metryki z tzw. sygnatura (+,-) ,a w drugim - ze sygnatura (-,+). W kazdym razie konsekwencja uzycia takich metryk (w obu przypadkach mamy tzw. przestrzen Minkowskiego) jest to, iz kwadrat czasu wchodzi do wyrazenia na interwal czasoprzestrzenny ze znakiem przeciwnym, niz kwadrat odleglosci przestrzennej (w tym przypadku "x").





TEMATY PRAC DYPLOMOWYCH:

Tematy prac licencjackich i magisterskich












Some links :

Instytut Informatyki Uniwersytetu Pedagogicznego w Krakowie

Instytut Fizyki Uniwersytetu Pedagogicznego w Krakowie

Instytut Matematyki Uniwersytetu Pedagogicznego w Krakowie

Instytut Techniki Uniwersytetu Pedagogicznego w Krakowie

Wydział Matematyczno-Fizyczno-Techniczny Uniwersytetu Pedagogicznego w Krakowie

Oddzial Krakowski Polskiego Towarzystwa Fizycznego

Strona o Wystawie "Fizyka blizej nas" - Krakow, Planty (ul. Golebia - sw. Anny), 10 maja - 31 lipca 2011 r. (tak sie sklada, ze bralem udzial w przygotowaniu tej Wystawy)

Association for Symbolic Logic ASL

9th International ISAAC Congress

Instytut Fizyki Uniwersytetu Jagiellońskiego

Wydzial Fizyki, Astronomii i Informatyki Stosowanej Uniwersytetu Jagiellońskiego

baza preprintow arXiv

COMS: Conference Management System - the advertisements on the conferences

the informational service "UK Nonlinear News" with news concerning "nonlinear" branches of sciences: the advertisements on the scientific events, the offers of jobs in "nonlinear" branches of sciences, some important publications etc.

Wydział Fizyki Uniwersytetu Warszawskiego

Polskie Towarzystwo Fizyczne (Polish Physical Society)

Polskie Towarzystwo Matematyczne (Polish Mathematical Society)

Physics World

metody numeryczne

kurs jezyka C++




: UTC + 1




Some forgotten outstanding Polish scientists:

Jan Czochralski (1885 - 1953) - Polish metallurgist, chemist and researcher in materials sciences. The Professor of Warsaw University of Technology. He is known mainly from his method of single crystal growing, world wide used, so-called, "Czochralski method", which was published 97 years ago. Owing to this method, among others, single silicon crystals, used for production of microprocessors, are being obtained. He has been called as "forefather of electronics". Just recently, he and his huge contribution into developing of electronics, have been reminded and on 17th December 2012 Polish Parliament (Sejm RP) voted for proclaiming 2013 the Year of Jan Czochralski.

(on the basis of:

the website on Jan Czochralski's life and works, developed by Czochralski's Family

another website on Jan Czochralski's life and works )

a broadcast on Jan Czochralski in Channel 1 of Polish Radio - 2nd June 2013 (in Polish)



Wladyslaw (Ladislas) Natanson (1864 - 1937) - Polish physicist. The Professor of Jagiellonian University in Krakow. He discovered the quantum statistics of particles, rediscovered independently 13 years later, by Satyendra Bose, developed later by Albert Einstein and called usually, as Bose-Einstein statistics. Natanson's paper including this statistics was published in 1911: W. Natanson, Physicalische Zeitschrift 12, 659 (1911). Natanson published also later in Polish another paper, devoted to this problem: "Principles of radiation theory": W. Natanson, Mathematical and Physical Letters 29, 1-232, Jagiellonian University (1912).

(on the basis of:

the website on outstanding Polish physicists (among others on Władysław Natanson) (in Polish)

an article of Prof. Józef Spałek (Marian Smoluchowski Institute of Physics of Jagiellonian University in Kraków), on Wladyslaw Natanson's discovery of (Natanson-)Bose-Einstein statistics (in Polish)

the article "WLADYSLAW NATANSON (1864-1937) For the 110th anniversary of formulation of the thermodynamics of irreversible processes and the 95th anniversary of formulation of quantum statistics" of Prof. Bronislaw Sredniawa (Marian Smoluchowski Institute of Physics of Jagiellonian University in Kraków), published in: "The Old and New Concepts of Physics", vol. IV, No 4, 705 (2007) (IN ENGLISH) )

Another article, including a comparison of Natanson's results and Bose's and Einstein's results (The Author has showed that the mode of calculating the distribution of indistinguishable particles, explained by Natanson, is the same as the statistics published 13 years later by Bose.):
Bogdan Lange, "Natanson's Statistics versus Bose-Einstein Statistics as the Basis For Theory-Cognitive Quantum Mechanics". Physics Essays: September 1997, Vol. 10, No. 3, pp. 524-527. DOI: http://dx.doi.org/10.4006/1.3036440

Other article, where one of Natanson's papers is cited:
C. Feiler, M. Buser, E. Kajari, W.P. Schleich, E.M. Rasel, R.F. O’Connell, "New Frontiers at the Interface of General Relativity and Quantum Optics", Space Sci. Rev. (2009) 148: 123–147; DOI 10.1007/s11214-009-9613-7



Rudolf Weigl (1883 - 1957) - Polish microbiologist and zoologist. The Professor of Lwow University in Lwow (in English: "Lvov", it belonged to Poland, before World War II - the same Lwow, where, at that time, among others, the most outstanding Polish mathematician, Stefan Banach was working; later, during German-Nazi occupation of Lwow, Stefan Banach was working in Institute of Weigl and owing to it, he prevented the arresting by Germans - more on Stefan Banach's life and works on this website ). He discovered the first effective vaccine against typhus. He was also nominated for the Nobel Prize in Physiology or Medicine.

(on the basis of:

the website, which includes links to many articles on Rudolf Weigl's life and works (mainly in Polish, some of them are written in English, German, Russian or Ukrainian) )




Witelon (Vitelo) (1230 - about 1314) - the first known Polish physicist, mathematician and natural scientist and simultaneously, the first wide known Polish scientist. In his work "Optics" (known as "Perspectiva"), he wrote about himself: "Filius Thuringorum et Polonorum" (A son of Turingists and Polish). He was engaged in optics and investigated, among others, the action of human eye: he distinguished the mechanism of action of eye and subconscious functionality of brain. Hence, he is recognized as a precursor of psychology. His work "Perspectiva" was used by Leonardo da Vinci, Nicholaus Copernicus and Johannes Kepler. Kepler wrote his own work entitled "Ad Vitellonem Paralipomena" ("A Supplement to Vitelon's work").

(on the basis of: the article on Vitelo's life and works (in Polish) )








Konsultacje w roku akademickim 2023/2024 - online lub pokój 411N (Nowy Budynek Uniwersytetu Pedagogicznego):

terminy podane na stronie Instytutu https://ii.uken.krakow.pl/pracownicy-up/lukasz-t-stepien/ , lub ewentualnie, do uzgodnienia via e-mail










  pokoj 411N, tel. +48 12 662-78-54,
  (ewentualnie, proszę pytać w pokoju 402N,   tel. +48 12 662-78-43, +48 12 662-78-44),            



adresy e-mail (prosze w pierwszej kolejnosci pisac na pierwszy adres e-mail):

      e-mail            e-mail

PROSZE NIE UZYWAC W MAILACH POLSKICH LITER.




Flag Counter


Ta strona została utworzona przy użyciu m.in. programu Extra Page 2.1 autorstwa Tomasza Majewskiego.
Informacje o programie i sam program można ściągnąć ze strony http://www.extrapage.com . Deklaracja dostępności cyfrowej